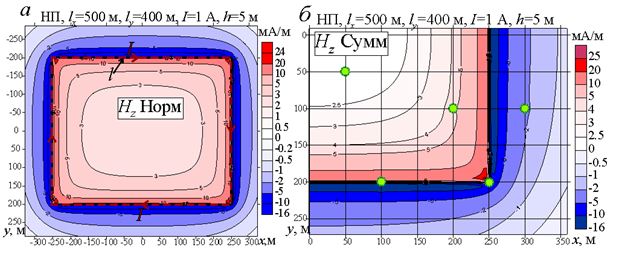Figure 1: Component maps
Figure 2: Component map
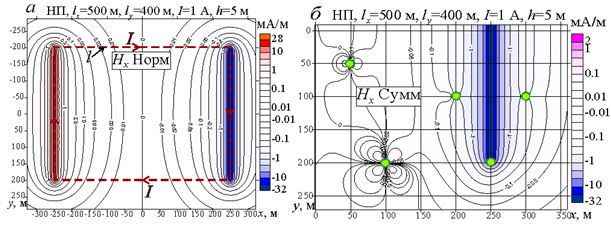Figure 3: Component maps
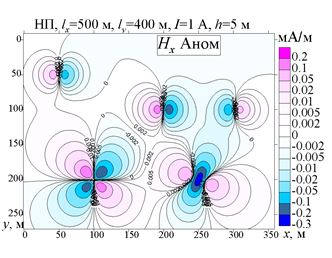Figure 4: Component map

In recent years, many studies have been conducted on the use of unmanned aerial vehicles (UAVs) in electrical and magnetic exploration. Some of the results of such studies have been published, for example, in the works [1,2,6]. This paper presents the results of mathematical modeling for the following conditions. A rectangular line l of electric current I ("rectangular loop") lies on the boundary S of a homogeneous lower conducting half-space V2 and an upper half-space V1 (air). Current I is the exciter of a normal magnetic field . In the half-space V2 at small depths from the surface S there are five local spherical objects with increased magnetic permeability μ. These objects are the exciters of the anomalous magnetic field . Total magnetic field

In the mathematical modeling, the Cartesian components of the fields were calculated in the half-space V1 at a height h above the boundary S. The method for calculating the influence of local objects on a constant and variable field is given in the works [3-5].

Note also that (at this stage) the calculation results given below are obtained for direct current I and a constant magnetic field. But it is obvious that these results will remain valid for the components of the low-frequency harmonically changing field when measuring the reactive components of the magnetic field changing in phase or in antiphase with the current I. Unlike the similar model for the magnetic field of alternating current I, the expressions for the constant magnetic field are elementary functions, and not improper integrals in the sense of the principal value.

Figure 1a shows the map (at height h=5 m) and the position of the rectangular loop in the plane S. It is clear that above the line l of the current I component changes sign, and the magnitude decreases with distance from line l.

Figure 1

In Figure 1, b, where the map is shown , the limits of change of coordinates x, y are less than in Figure 1, a. The green circles show the position in the plan of five local magnetized objects located in the lower half-space. In this figure we see that for the given parameters of the model, the influence of local objects on the map is practically unnoticeable. This is obviously due to the fact that when the field is excited rectangular line l current I absolute value

Figure 2 shows the component map Of course, on this map we see anomalies caused by the influence of all local objects. But when comparing the values in figures 1, a, 2 we see that indeed, as already noted, . Of course, in mathematical modeling the values could be calculated with very high accuracy. And to clarify the question of whether it is possible in practice to determine ensure high measurement accuracy calculations and subsequent calculation of the difference . Experimental studies are needed.

Figure 2

Figure 3

Figure 3a shows a map of the horizontal component . According to the Biot-Savart-Laplace law, the maximum values we observe those sections of the contour l, the current I along which is collinear to the direction of the Y axis. In the central part of the map, the inequality (see Figure 1, a). At the same time, it is very important that the magnetization of local objects and the values . It depends, of course, not only on the component , and from all components of the total field , including from components . Therefore, the influence of local objects on the component manifests itself much more "noticeably" than such an influence on the component .

We see this in Figure 3, b, which shows the map . This map clearly shows two anomalies caused by magnetized local objects. These are the objects whose centers have coordinates x=50 m, y=50 m and x=100 m, y=200 m. That is, when a normal magnetic field is excited by a rectangular current loop I, compared to component more "sensitive" to the influence of local magnetized objects. In addition, some influence on the component provide local objects with coordinates of centers x=200 m, y=100 m and x=300 m, y=100 m.

Similar results were, of course, obtained for the other horizontal y - component of the magnetic field. Only the maximum values in this case we observe those sections of the contour l, the current I along which is collinear with the direction of the X axis.

Figure 4

Figure 4 shows the component map . Note that for the given model parameters, the values reach tenths of mA/m, which is greater than the values in the central part of the map in Figure 3, a.

The simulation results showed that when a magnetic field is excited by an ungrounded loop and measurements are made using a UAV when searching for local magnetic objects, the horizontal components of the magnetic field are more “sensitive” to the influence of these objects.

  1. Davydenko SYu, Tereshkin SA, Davydenko AYu, Snopkov SV, Parshin AV, avydenko Yu.A (2021) Application of UAVs and Ground-Based Geophysical Methods in the Study of the Ancient Metallurgical Complex at the Barun-Khal II Site (Western Baikal Region) // Geoarchaeology and Archaeological Mineralogy. Miass: Imin UB RAS, 8: 35-40.
  2. Davydenko YuA, Bashkeev AS, Yakovlev SV, Shkirya MS, Bukhalov SV, Krainova EA, et al. (2021) First results of testing UAV-MPP technology on Lake Baikal. VIII All-Russian school-seminar EMZ-2021, Moscow, October 4-9.
  3. Karinsky AD, Daev DS, Mazitova IK, Yudin MN (2016) Mathematical modeling of the influence of local objects on the results of resistivity methods of electrical exploration. International scientific and practical conference "Theory and practice of exploration and production geophysics", Perm, November 24-6,ss pp. 122-6.
  4. Karinsky AD, Daev DS (2017) Influence of local objects on the results of electrical exploration using the resistivity method; experience of mathematical modeling. // "Geophysics". Scientific and technical journal. 1: 35-44.
  5. Karinsky AD (2022) Influence of local objects on the results of some electrical exploration methods; data of mathematical modeling/. M., 82.
  6. Parshin AV (2020) Method of aerial electrical reconnaissance using a light unmanned aerial vehicle. Patent RU 2736956 C1.