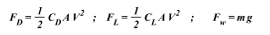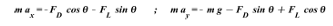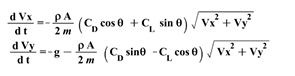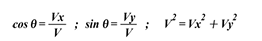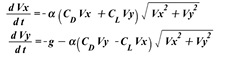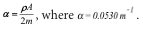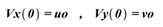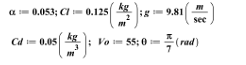Review Article
Volume-1 Issue-1, 2025
Investigate of Movement of the Cannonball in the Gas Along with the Friction Force
-
Received Date: May 01, 2025
-
Accepted Date: May 17, 2025
-
Published Date: May 24, 2025
Journal Information
Abstract
We consider a ball moving in the xy-plane spinning about an axis perpendicular to the plain on the motion. The typical trajectory of the ball is shown in figure 1
Key words
cannonball, friction Force, aerodynamics, dynamics
| Figure 1: Throw a bullet from a Height |
| Figure 2: A comparison between AYM and Numerical solution |
| Figure 3: A comparison between AYM and Numerical solution |
Mathematical formulation of the problem
the force acting on the ball are Drag force,(FD), the lift force(F1), and the gravitation force,(FW) as follows
The equatation of motion takes the form:
After substituting Eqs.(1) in to Eqs.(2),We have as follows
We can write:
So, the equations can be written entirely as a system set of nonlinear differeential equations for the velocity ad follows:
and value
Initial conditions as:
By selecting the physical values at below:
AYM solution process (Akbari Yasna’s Method) Output of the solution process by new approach AYM (Akbari Yasna’s Method) for set of nonlinear differential equations Eqs(5), according to the initial conditions Eqs.(6) and physical values Eq.(7), the solutions. set of the non-defferential equations is obtained as follows:
Comparing the achieved solutions by Numerical Method order Runge-Kutta and AYM (Akbari Yasna’s Method)
In this article, we proved that with this new method, all kinds of complex practical problems related to nonlinear differential equations in the designs for motions of a solid in a fluid can be easily solved analytically. Obviously, most of the phenomena in dunamics and aerodynamics are nonlinear so it is quite difficult to study and analyze nonlinear mathematical equations in this area, also we wanted to demonstrate the strength, capability and flexibility of the new AYM methods(Akbari-Yasna Methods).This Methods is newly created and it can have high power in analytical solution of all kinds of industrial and practical problems in engineering fields and basic sciences for complex nonlinear differential equations
Acknowledgment, History of AGM , ASM , AYM , AKLM , MR.AM and IAM methods: AGM (Akbari-Ganji Methods), ASM (Akbari-Sara’s Method) , AYM (Akbari-Yasna’s Method) AKLM (Akbari Kalantari Leila Method), MR.AM (MohammadReza Akbari Method)and IAM ( Integral Akbari Methods), have been invented mainly by Mohammadreza Akbari (M.R.Akbari) in order to provide a good service for researchers who are a pioneer in the field of nonlinear differential equations
*AGM method Akbari Ganji method has been invented mainly by Mohammadreza Akbari in 2014. Noting that Prof. Davood Domairy Ganji co-operated in this project.
method (Akbari Sara's Method) has been created by Mohammadreza Akbari on 22 of August, in 2019.
method (Akbari Yasna's Method) has been created by Mohammadreza Akbari on 12 of April, in 2020.
*AKLMmethod (Akbari Kalantari Leila Method)has been created by Mohammadreza Akbari on 22 of August, in 2020.
*MR.AM method (MohammadReza Akbari Method)has been created by Mohammadreza Akbari on 10 of November, in 2020.
*IAMmethod (Integral Akbari Method)has been created by Mohammadreza Akbari on 5 of February, in 2021.
References
- Book Nonlinear Dynamic in Engineering by Akbari-Ganji's Method ISBN-13: 978-1514401699, ISBN-10: 151440169X.
- MR Akbari, Sara Akbari, Esmaeil Kalantari (2020) ‘Akbari Ganji s method “AGM” to chemical reactor design for non-isothernal and non-adiabatic of mixed flow reactors'Journal of Chemical Engineering and Materials Science 11: 1-9.
- MR Akbati,DD Ganji,M Nimafar (2014)"Signification progress" in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach", Frontiers of Mechanical Engineering Journal.
- AK Rostami, MR Akbari, DD Ganji, S Heydari (2014) Investigating Jeffery-Hamel flow with high maganetic field and nanoparticle by HPM and AGM, Cent. Eur. J. Eng 4: 357-70.
- MR Akbari, DD Ganji, A Majidian, AR Ahmadi (2014) "Solving nonlinear differential equations of Vanderpol, Rayleigh and Duffing by AGM", Frontiers of Mechanical Engineering
- DD Ganji, MR Akbari, AR Goltabar (2014) “Dynamic Vibration Analysis for Non-linear Partial Differential Equation of the Beam - columns with Shear Deformation and Rotary Inertia by AGM”, Development and Applications of Oceanic Engineering (DAOE), ISSN Online: 2325-3762.
- MR Akbari, DD Ganji, AR Ahmadi, Sayyid H Hashemi kachapi (2014) "Analyzing the Nonlinear Vibrational wave differential equation for the simplified model of Tower cranes by (AGM)" Frontiers of Mechanical Engineering Volume 9: 58-70.
- MR Akbari, M Nimafar, DD Ganji, MM Akbarzade (2014) "Scruiny of non-linear differential equations Euler Bernoulli" beam with large rotational deviation by AGM” Springer.
- M. R. Akbari, Sara Akbari , Esmaeil Kalantari, “A Study about Exothermic Chemical Reactor by ASM Approach Strategy”Crimson Publishers Wings to the Research,Published, March 17, 2020.
Artcle Information
Review Article
Received Date: May 01, 2025
Accepted Date: May 17, 2025
Published Date: May 24, 2025
World Journal of Advances in Applied Physics and Mathematical Theories
Volume 1 | Issue 1
Citation
M.R Akbari, Sara Akbari, Esmaeil Kalantari (2025) Investigate of Movement of the Cannonball in the Gas Along with the Friction Force. World J Adv Appl Phys Phys Math eo 1: 105
Copyright
©2025 M.R Akbari. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

doi: japm.2025.1.105