
Review Article
Volume-1 Issue-2, 2025
A short proof and Refinements of Minkowskis in equality
-
Received Date: July 06, 2025
-
Accepted Date: July 23, 2025
-
Published Date: July 30, 2025
Journal Information
Abstract
Inthispaper, inspiredbytheworkof [4],[7]and[8-10],wearegongingtopresentashortproof ofthewell-knownMinkowskisinequalityandgiveaninterpolationandare nementof it.
Key words
Minkowskisinequality;convexfunctions;re nement; interpolation
| Figure 1: Throw a bullet from a Height |
| Figure 2: A comparison between AYM and Numerical solution |
| Figure 3: A comparison between AYM and Numerical solution |
Introduction
In[7],theauthorusedanelementarymethodgaveashortproofofthewell-knownHoldersinequality:
whereallak bk>0and
=1withp q>1 Theequalityholdswhen
forallk j=1 2 nMoreover,ifp=q=2,inequality(1)reducestothewell-knownCauchysinequality:
In[4,8-10], theauthorsconsideredthefollowingfunction
andprovedthat for0 t1 < t2 << tk 1 thenthe following interpolationandre nementof the Holdersinequality
Like Holders in equality, the well-known Minkowskis in equality plays also an important rule in themath ematical and physics research elds and literatures. There are the most important, interesting,useful and elementary in equalities in mathematics,physics and other research elds. It plays an important role in math ematics and physics research elds and has great potential in the future research.There were many research papers devoted to the generalizations,re nements and applications of these two important inequalities.For examples, were fert other references in[1-11]and there referencescited in them. Since their importance and applicationpotential both in theory and practical applications, in this paper, inspired by the works of [4,7 10],weare going to present a short proof of the well-known Minkowskis inequality and give are nement andan inter polation of it.Ourresults are new and givenb elow.
Theorem 1. If ai bi>0 i=12 np>0, thenforp 1,wehave
and for 0< p 1,we have
Theorem2. DeneaC functiong(x)asfollows
Then for p=1,g(x)
(ak+bk) g(0)=constant.
For p>1 g(x) 0 and for0 x1< x2< < xm 1,the following inequalities are re nementsand interpolation of g(x):
For 0< p< 1g(x) 0 and for0 x1< x2< < xm 1, the following in equalities are re nements and inter polations of g(x).
Moreover,
and g (x) 0 if and only if g(1)=g(0), in this case,g(x) 0 and g(x) g(0)=constant
Proof of Theorem1. For1<=m<=n set x=a m and define
where
Hence
Solvingequationf(x)=0,weget
and after some calculations,we obtain
It follows from equation(9)and x= am that
That is 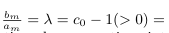
Since
wegetfrom(8) (9)that
If p=1, thenfm(x) 0, inthiscase, (4)and(5)becomes equality for all ak>0 bk>0 1< k< n.
If p>1, then fm(x)>0 for all x>0,hence fm(x) achieves its minimum at x=x where x satisfies fm(x)=0 in this case in equality(4) holds.
If 0< p< 1,then fm(x)< 0 for all x> 0,hence fm(x)achieves its maximum at x=x where x satisfies fm(x)=0 in this case, inequality (5) holds.Theorem 1 is proved.
Proof of Theorem 2. It follows from the expression of g(x) that
By Theorem 1, if p=1, then
If p > 1, then g(1) g(0),with
equality holds if and only if
Inthis
case,
Then (7) is an interpolation and a re nement of (4).
If 0 < p < 1, then g(1) g(0), with
equality holds if and only if
in
this case,
Declarations
Ethical Approval
Consent to Publish.
Funding
Not Applicable
Data availability
No data was used for the research described in the article.
Conflict of Interest
Not Applicable
References
- A.Abramovich, J.Pecaric and S.Varosanec, Continuous sharping of Holders and Minkoeskis inequali ties, Mathmatical Inequalities and Applications, 8(2)(2005), 179190.
- E.F.Beckenbach and R.Bellman, Inequalities, Springer-Verlag, Berlin, 1961.
- G.Hardy, J.E.Littlewood and G.Polya, Inequalities, Cambridge University Press, 1934.
- Y.Kim and X.Yang, Generalizations and re nements of Holders inequality, Applied Mathematics Let ters, 25, (2012) 10941097.
- U.S.Kirmaci, On generalizations of Holders and Minkowskis inequalities, Mathematical Sciences and Applications E-Notes, 11(4), (2023), 213225.
- L.Nikolova, L.Persson and S.Varosanec, Some new re nements of the Young, Holder, and Minkowski inequalities, Jpurnal of Inequalities and Applications,2023;28.
- K.Razminia, Holders inequality revisited, The Mathemtical Gazette, 103.35, (2019), 512514.
- X.Yang, A generalization of Holder inequality, J.Math.Anal.Appl., 247 (2000), 328330.
- X.Yang, Holders Inequality, Applied Mathematics Letter, 16, (2003), 897903.
- X.Yang, A note on Holder inequality, Applied Mathematics and Computation,134 (2003), 319322.
- C.J.Zhao and W.S.Cheung, On Minkowskis inequality and its application, J.Inequal.Appl. 71, (2011), 2011
Artcle Information
Review Article
Received Date: July 06, 2025
Accepted Date: July 23, 2025
Published Date: July 30, 2025
World Journal of Advances in Applied Physics and Mathematical Theories
Volume 1 | Issue 2
Citation
Youla Yang (2025) A Short Proof and Refinrments of Minkowski’s Inequality. World J Adv Appl Phys Math Theo 1:202
Copyright
©2025 Youla Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

doi: japm.2025.1.202

